Modern Physics
Answer: 5,795 K
λmax = b/T; so T = b / λ(max) = 2,897,000 nm·K / 500 nm = 5,795 K
1 nm = 1 x 10-9 m
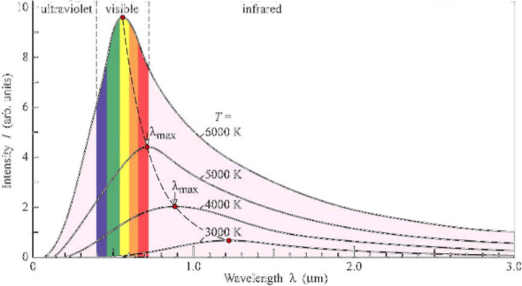
The figure below illustrates this very convenient property of radiation.
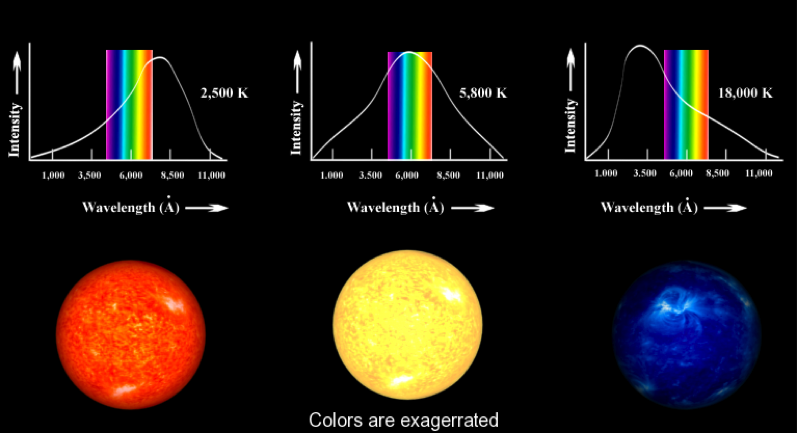
Above: Image from: http://docs.kde.org/stable/en/kdeedu/kstars/ai-colorandtemp.html
The white curves in the top graphs show the brightness of the stars against a visible light spectrum. The bottom images show colors matching each brightness distribution curve.
Another example:
Betelgeuse is a red super giant star in the constellation of Orion and the eighth brightest star in the sky. It’s blackbody radiation spectrum peaks at around 970 nm. What is its surface temperature? Is it hotter or cooler than our sun?
T = 2,897,000 / λmax
Applying it to Betelgeuse:
T = 2,897,000/970 = 2,987 K
Our Sun has a surface temperature of 5,795 K, almost twice as hot as the red star Betelgeuse.
Answer: 20,000 K
Solution:
T = 2,897,000/145 = 19,979 K
(round to 20,000 because there are only 3 significant digits)
Rigel is about 3.5 times brighter than our Sun.
Whenever you see stars in the sky you now know that the red ones are cooler, and the blue/white ones are hotter than our yellow Sun.
© 2013 by Wheeling Jesuit University/Center for Educational Technologies®. 316 Washington Ave., Wheeling, WV 26003-6243. All rights reserved. Privacy Policy and Terms of Use.