Kepler's Three Laws of Planetary Motion

 

Under the force of gravity, all objects in orbital motion obey a series of laws first proposed by Johannes Kepler in 1609 and 1619. These are his, now famous, three laws of orbital motion.

 

1. All planetary objects move in elliptical orbits

2. Objects sweep out equal areas in equal time

3. P² ~ a³ (the square of the period is proportional to the cube of the semi major axis or average distance from the Sun.)

 

These laws apply to objects in orbit around the Earth, the Sun, Jupiter, other stars, galaxies, and even clusters of galaxies. Let’s explore them one at a time to see what they mean. To explore these more fully, use the Planetary Orbit Simulator.

Kepler's 1st Law: All objects orbit in elliptical orbits.

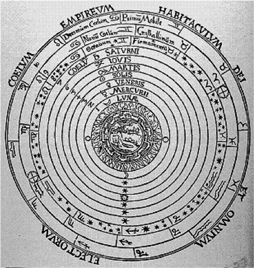For many centuries it was believed that the heavens were the realm of gods and so were perfect and pristine. Earth was viewed as far less than perfect (the realm of mere mortals). For this reason, it was believed that all orbits of the planets were perfect circles. In those days, scientific fact was often arrived at by what reasoning seemed most elegant as opposed to careful observation and experimentation. Around 300 BC, Aristotle proposed that the Earth was a perfect sphere held stationary in space while planets and stars moved in spherical orbits around it.

 

Ptolemy (2nd century AD) did not question this belief and built his astronomical models of the solar system and the universe on the same assumption of perfect spherical shells and circular orbits. This caused astronomers problems for more than 1,000 years because actual observations of the planets didn’t agree with circular motions.

 

It was not until the early 16th century that Johannes Kepler, working from detailed tracking of planetary orbits by Tycho Brahe, finally gave up trying to fit planetary orbits into perfect circles and developed a model whereby planets orbit in elliptical paths. This was a huge breakthrough in scientific thinking, basing understanding on observations, not idealized concepts.

 

Ellipses are two dimensional ovals built with two foci. A circle is actually a type of ellipse where the two foci coincide.

 

 

Try This!

 

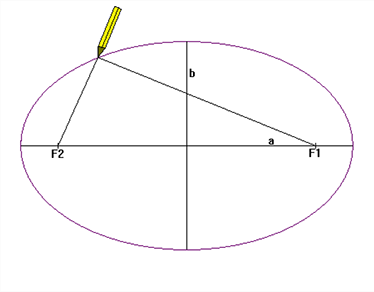You can easily construct an ellipse on a sheet of paper. Put push pins in the paper some distance apart. Now take a piece of string whose length is roughly twice the separation of the push pins. Attach the string at each end to the push pins. Now, with a pencil, stretch the string into a triangle shape (see diagram). Continuing to keep the string taut with the pencil, draw all around the pins. You have just drawn an ellipse with the push pins as its two foci. In space, a large object (star) would be located at one foci (it doesn’t matter which one) and a planet would move along the elliptical path you drew. Now experiment with different length strings and different separations between the pins. What shape do you get with only one pin? Use the Planetary Orbit Simulator to experiment further. http://astro.unl.edu/naap/pos/animations/kepler.html