Roller Coaster Physics

We can say that the sum of potential energy plus kinetic energy remains constant at any point in time, again, for a closed system. Let’s take a look at how this applies in one of the most personally exhilarating applications of physics.

​Left: Dragon Khan roller-coaster in Universal Port Aventura park in Spain, Wikipedia

 

​
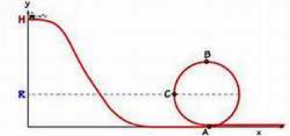
A 100 kg roller coaster that does a loop-d-loop must be designed such that the coaster stays on the tracks at all times especially when it is upside down. Using equation 2.4 above, we can write:

 

PE_H + KE_H = PE_A + KE_A = PE_B + KE_B = PE_C +KE_C

 

That is, the sum of the potential and kinetic energy will be the same for all points H, A, B and C on the roller coaster track assuming the ideal case where no energy is lost due to friction. PE can be converted into KE and back, but the sum will always be a constant.

 

Initially, at point H where y = 20 m above the ground, the roller coaster has no kinetic energy but lots of potential energy. We know it has no kinetic energy because its velocity = 0! Its potential energy can be calculated from Equation 3.3 as:

 

PE = mgh = 100 kg • 9.8 m/s² • 20 m = 19,600 J

 

At the bottom of the roller coaster track (point A), the coaster has no potential energy (h = 0) and lots of kinetic energy. In fact, it has a maximum of kinetic energy and so a maximum velocity. Its kinetic energy can be described as:

 

KE = ½ mv² = ½ * 100 kg * v² (m/s)²

But what is the coaster’s velocity?

 

Since we know that PE + KE = constant, we know that the KE at the bottom is just equal to the potential energy of the coaster at the top (PE = 19,600 J), and the maximum value of the PE equals the maximum value of KE (assuming there is no friction).

(Left: Rollercoaster © Zechal - Fotolia.com)

 

 

PE = 19,600 J = KE = ½ mv²

19,600 J = ½ * 100 * v² = 50 v²

and so v = (19,600 J/50)^½ = 19.8 m/s

 

For the roller coaster at any point on the track:

    ETotal = PE + KE = Potential Energy at maximum height, H.

 

mgH = mgy + ½ mv²

 

where y = the height of the roller coaster at that point.

 

Collecting terms of the last equation gives us a general equation for the velocity of a roller coaster at any point – not very important in the scheme of things, but something you derived and now understand:

 

​velocity squared = 2 x gravity x(maximum height - height at any given point) v² = 2g(H-y)