Equation

velocity =

acceleration x time

 

v = gt

 

Equation

distance traveled =  ½ x acceleration x times squared

 

d = ½ gt²

Gravity and Acceleration

 

The force of gravity has an associated acceleration. Gravity ACCELERATES objects. In the early 1600’s Galileo Galilee theorized that in the absence of air, all things would fall toward the Earth with the same acceleration. At its surface, Earth’s huge mass accelerates objects toward it at a rate of 9.8 m/s² or, said another way, 9.8 meters per second per second. So, ignoring atmospheric drag for a moment, an object falling toward the Earth will travel at a speed of 9.8 m/s after its first second of free fall, 19.6 m/s after its 2nd second of its fall, and so on. We saw earlier equations for the velocity and distance traveled for an accelerating body:

 

v = at    and    d = ½ at²

 

Since gravity is an accelerating force, we can simply replace “a” in these equations with “g” the acceleration due to gravity.

 

v = gt    and    d = ½ gt²

 

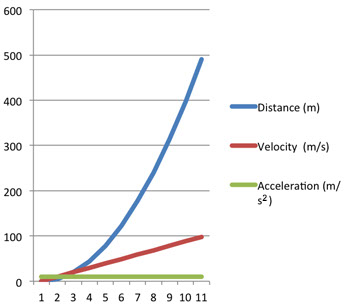
Doing this results in the following table and chart:

 

​​Time(s)

012345678910Distance(m)

04.919.644.178.4122.5176.4240.1313.6396.9490Velocity(m/s)

09.819.629.439.24958.868.678.488.298Acceleration(m/s²)

9.89.89.89.89.89.89.89.89.89.89.8

Notice that the acceleration stays constant at 9.8 m/s², because although the acceleration of gravity varies on Earth, it is the roughly same anywhere on Earth and above it (until you reach great heights). If acceleration is flat and unchanging as is the case here, then velocity increases at a constant rate and distance increases at an accelerating rate. That is because v is proportional to t, and d is proportional to t².

 

Lunar Gravity

 

Each planet has its own value of “g” – for the Moon it is 1.6 m/s². And for Mars “g” is 3.8 m/s².  Because lunar gravity is so small astronauts could lope across the lunar surface, with long, almost floating strides – here is a NASA video of Apollo astronauts walking, skipping and singing. And in this snippet astronaut Jack Schmidt falls, almost in slow motion.