Description

 

US Geological Survey photograph by B. ChouetWitnessing a volcanic eruption should be on everyone's bucket list, but from not too close.  For a small eruption, such as this one at Stromboli Volcano in the Mediterranean Sea, hot volcanic rocks are ejected and then fall back to Earth following a trajectory determined by gravity.

 

Living on the Earth, it is a part of our daily lives to expect all things to fall to the ground, or more generally, toward the center of the Earth. This, of course, is a result of Earth’s huge mass and resulting gravitational pull. The force of gravity falls off very gradually as we move away from the center of the Earth (e.g. top of a mountain or in a commercial airliner), but these distances are very small compared to the size of the Earth, and so for all practical purposes, the acceleration of gravity is the same, 9.8 m/s², regardless of our altitude.

 

A projectile is an object whose trajectory is determined by the force of gravity alone. Throw a baseball, shoot a free throw, drop a penny down a well, shoot a watermelon with a giant catapult; once the initial force has been applied, and the object is in free flight, it is a projectile whose motion is governed solely by the force of gravity (let’s ignore air resistance for now).

 

As we have seen, the pull of gravity is constant near the surface of the Earth, so the acceleration due to gravity is a constant acceleration. Once the projectile is launched/fired/thrown/dropped, gravity begins pulling on it to slow its rise away from the Earth and pull it back down, as if it were attached to a spring anchored at the center of the Earth. Since we know the force of gravity very accurately, knowing the initial magnitude and direction of the launching force (yes, force is a vector!), we can calculate the height the projectile will reach, its velocity at any time during its flight, and its distance traveled.

 

Projectiles

 

Let’s begin with a cannon fired horizontally from the top of a mountain. Again, neglecting drag, the canon ball will follow a parabolic trajectory down to the ground. This path is created by the combination of the horizontally applied force on the cannon ball and the vertical force of gravity. The two forces act completely independently of one another so that the cannon ball reaches the ground in the same amount of time independent of its initial horizontal velocity.

 

​Diagram from: http://www.physicsclassroom.com/Class/vectors/u3l2a.cfm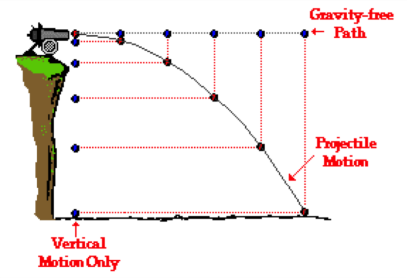

 

The Italian scientist Galileo in the early 1500s first realized that we can treat the horizontal and vertical components of the cannonball’s movement separately as follows:

 

Horizontal Motion:

 

​   x = v_ixt + ½ a_xt²      v_fx = v_ix + a_xt

 

Where v_ix is the initial velocity in the x direction, and v_fx is the final velocity in the x direction. Usually v_ix is zero, so the first term of Equations 1.11 and 1.12 disappear and they are the same as Equations 1.7 and 1.5.

 

The vertical component is treated the same way, except that the acceleration, a, is replaced by g, the acceleration of gravity, since that is the downward force on the cannonball:

 

​   y = v_iyt + ½ gt²     v_fy = v_iy + gt