Forces and Motion
Orbital Motion
Kepler's 2nd Law: Objects sweep out equal areas in equal time.
As a planet, moon, or satellite orbits its central body along an elliptical path, it ventures both closer and further from its parent body during a single orbit. When the object is moving away from its parent body, it is fighting the pull of gravity and slows down. When it is moving toward its parent body, it gains energy and speeds up, accelerated by gravity. It does this in such a way that it sweeps out equal pie-shaped areas in its orbital plane in equal amounts of time no matter where in its orbit it is or how fast it is going. In this illustration each color triangle has the same area, and it takes the same time for the planet to move across. You can use the Planetary Orbit Simulator to demonstrate this.
Right: Illustration captured from UNL Planetary Orbit Simulator
Equation
P2 ~ a3
1.15
Teachers’ Guide* to Kepler’s Laws:
http://www-spof.gsfc.nasa.gov/stargaze/Kep3laws.htm
*great for students, too!
Kepler's 3rd Law:
P2 ~ a3
(the square of the period, p, is proportional to the cube of the semi major axis, a, which is the average distance of an object from the Sun).
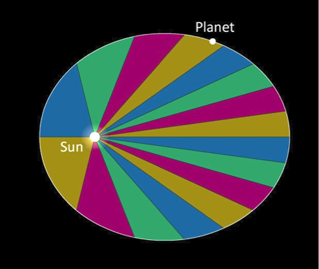
Left: Illustration captured from UNL Planetary Orbit Simulator
Kepler’s third law attempts to quantify planetary motion. The law as written here applies to all orbiting objects (e.g. satellites around the Earth, moons around Jupiter, double star systems). The “ ~ ” means “is proportional to”. It turns out that if we use the right units of measure, in this case years for P and AU for a, then we can replace the “ ~ ” with an “=” sign when calculating planetary orbits in our own solar system. In the diagram above Kepler’s 3rd Law is plotted for M, V, E and M again - the planets Mercury, Venus, Earth and Mars. Mars has a period of 1.88 years (that is how long it takes to go around the Sun one time) and the distance is measured in astronomical units (1 AU equals the distance from Earth to the Sun, about 150,000,000 km). Mars is 1.52 AU from the Sun.
Answer: 29.7 years
P2 = a3 with p to be determined and a = 9.6 AU.
P2 = a3 = 9.63 = 885
p = 29.7 years
© 2013 by Wheeling Jesuit University/Center for Educational Technologies®. 316 Washington Ave., Wheeling, WV 26003-6243. All rights reserved. Privacy Policy and Terms of Use.