-
WHAT IS NASA PHYSICS?
-
MODULES
-
Forces and Motion
-
Conservation of Momentum & Energy
-
Temperature and Heat
-
Fluids
-
Optics
-
Electromagnetic Spectrum
-
Modern Physics
-
Anticipation Guide 7
-
Intro to Modern Physics
-
Blackbody Radiation
-
The Ultraviolet Catastrophe
-
The Photoelectric Effect
-
Bohr's Atom
-
Spectra
-
Radioactive Decay
-
Special Relativity (SR)
-
Simultaneity
-
Distance and Time
-
General Relativity
-
May the Forces be with You
-
Modern Physics Notebook
-
Assessment Problems 7
-
-
Useful Things
-
-
SITE MAP
Forces and Motion
-
Anticipation Guide
-
Speed and Velocity
-
Acceleration
-
Gravity
-
Projectile Motion
-
Orbital Motion
-
Newton's Laws of Motion
-
Assessment Problems
Equation
v = (GM/r)½
1.16
Reminder
G= 6.673 x 10-11 Nm2/kg2
Orbital Motion
Orbital Velocity
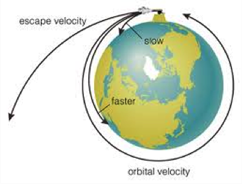
 As we have seen, an object must reach a critical tangential velocity in order to go into orbit around a planet. An object would continue in a straight line forever unless some force acted on it. This force is gravity. Gravity pulls. It pulls the potentially orbiting object towards the center of the planet.
As we have seen, an object must reach a critical tangential velocity in order to go into orbit around a planet. An object would continue in a straight line forever unless some force acted on it. This force is gravity. Gravity pulls. It pulls the potentially orbiting object towards the center of the planet.
Taking the example of the Earth and a satellite payload that was just launched, we want to send the payload fast enough tangentially or, in other words, perpendicular to the force of gravity such that it will always miss the Earth’s surface as it falls. To do this, it has to attain orbital velocity. For low Earth orbit, around 325 km in altitude, an object must travel about 28,000 km/hr in a direction perpendicular to the pull of gravity. How did we calculate this velocity?
Sir Isaac Newton provided the answer. He showed that: v = (GM/r)½
Remember that the exponent of ½ means to take the square root of the term inside the parentheses.
Notice that this velocity is independent of the mass of the satellite and only depends on the mass of the central body (Earth in this case) and the distance from the center of the Earth, r.
The average radius of the Earth at its equator is 6,378.15 km. Let’s add 300 km to this for an orbiting altitude, so r = 6,378 + 300 = 6,678 km. The mass of the Earth is 5.974 x 1024 kg. Converting to kg-m-s units, we get the following equation for v:
v = (6.673 x 10-11 Nm2/kg2 x 5.974 x 1024 kg/ 6.678 x 106m)½ = 7.726 km/s = 27,815 km/hr
Try This!
Calculate orbital velocities for the following bodies:
| Object | Mass (kg) | Radius (km) | Orbital Radius (km) | Orbital Velocity (km/s) |
| Moon | 7.36 x 1022 | 1,737 | 1,937 | |
| Mars | 6.42 x 1023 | 3,397 | 3,597 | |
| Sun | 2.00 x 1030 | 695,500 | 149.6 | |
| Neutron Star | 2.8 x 1030 | 20 | 220 | |
| Milky Way Galaxy | 1.16 x 1042 | 2.55 x 1017 | 2.55 x 1017 | |
| Basketball | 0.5 | 4.7 x 10-5 | 0.001 |
(Remember to click 'Fit to Page' in your printer settings).
© 2013 by Wheeling Jesuit University/Center for Educational Technologies®. 316 Washington Ave., Wheeling, WV 26003-6243. All rights reserved. Privacy Policy and Terms of Use.

